Triangles ⇒⇒ Exercise 7.1

Question 1

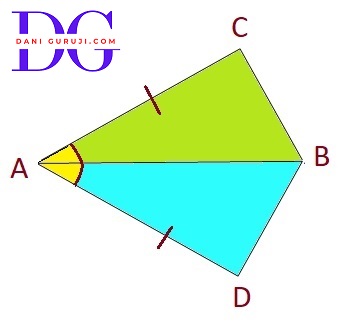
In quadrilateral ACBD, AC = AD and AB bisect $\angle A$ (see Fig.). Show that ΔABC $\cong$ ΔABD. What can you say about BC and BD?

Solution :

In quadrilateral ABCD we have s given that AC and AD are equal i.e. AC = AD and the line segment AB bisects A .

Consider the triangles Δ ABC and Δ ABD

⇒ AC = AD

( Given in the problem. )

⇒ $\angle $ CAB = $\angle $ DAB

( AB bisects $\angle $CAD, meaning it divides the angle into two equal parts. )

⇒ AB = AB

( This is a common side for both triangles. )

∴ ΔABC $\cong$ ΔABD

( by the SAS congruence rule. )

The Side-Angle-Side (SAS) congruence criterion. This theorem states that if two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of another triangle, then the two triangles are congruent.

Relationship Between BC and BD

Because we have proven that ΔABC $\cong$ ΔABD

we know that their corresponding parts are also equal.

Since BC and BD are corresponding sides of the two congruent triangles, we can say that BC = BD. (By C.P.C.T.)

BC and BD are of equal lengths by the rule of C.P.C.T

Question 2

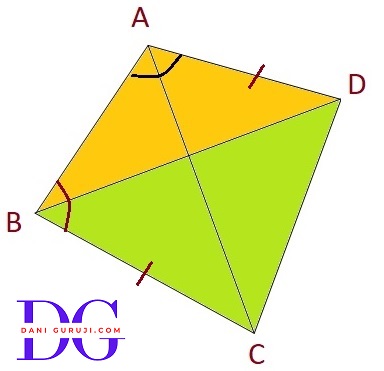
ABCD is a quadrilateral in which AD = BC and $\angle $DAB = $\angle $CBA. Prove that
(i)ΔABD $\cong$ ΔBAC
(ii) BD = AC
(iii) $\angle $ABD = $\angle $BAC

Solution :

(i): Proving Δ ABD $\cong$ Δ BAC

In quadrilateral ABCD we have AD = BC and $\angle $DAB = $\angle $CBA.

Consider the triangles Δ ABD and Δ BAC

⇒ AD = BC

( Given in the problem. )

⇒ $\angle $DAB = $\angle $CBA

( Given in the problem. )

⇒ AB = BA

( This is a common side for both triangles. )

∴ ΔABD $\cong$ ΔBAC

( by the SAS congruence rule. )

The Side-Angle-Side (SAS) congruence criterion. This theorem states that if two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of another triangle, then the two triangles are congruent.

Proving BD = AC

Because we have proven that ΔABD $\cong$ ΔBAC

we know that their corresponding parts are also equal.

Since BD and AC are corresponding sides of the two congruent triangles, we can say that BD = AC. (By C.P.C.T.)

BD and AC are of equal lengths by the rule of C.P.C.T

(iii) Proving $\angle $ABD = $\angle $BAC

Because we have proven that ΔABD $\cong$ ΔBAC

we know that their corresponding parts are also equal.

The angles $\angle $ABD and $\angle $BAC are corresponding angles in the two congruent triangles. , we can say that $\angle $ABD = $\angle $BAC. (By C.P.C.T.)

Question 3

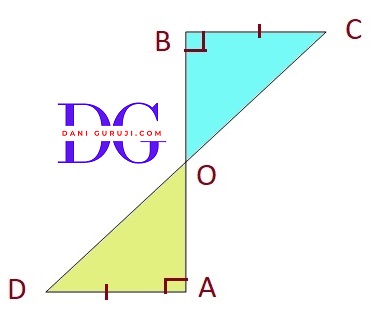
AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.

Solution :

From given figure, It is given that

AD and BC are equal perpendicular to AB. This means that

$\angle $DAB = $\angle $CBA = 90°

Consider the triangles Δ AOD and Δ BOC

⇒ AD = BC

( This is given in the problem statement. )

⇒ $\angle $DAB = $\angle $CBA

( Both are 90°. )

⇒ $\angle $AOD = $\angle $BOC

( These are vertically opposite angles, and vertically opposite angles are always equal. )

∴ ΔAOD $\cong$ ΔBOC

( by the AAS congruence rule. )

( According to the AAS (Angle-Angle-Side) congruence criterion, if two angles and a non-included side of one triangle are equal to the corresponding angles and non-included side of another triangle, then the two triangles are congruent.)

Proving BO = AO

Because we have proven that ΔAOD $\cong$ ΔBOC

we know that their corresponding parts are also equal.

Since BO and AO are corresponding sides of the two congruent triangles, we can say that BO = AO. (By C.P.C.T.)

Since we have shown that AO = BO, we have proven that the line segment CD divides AB into two equal halves.

Therefore, CD bisects AB and O is the mid-point of AB.

Question 4

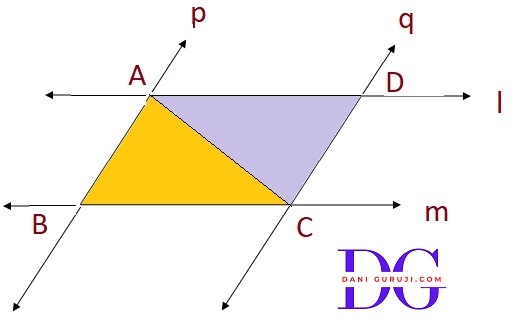
l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig.). Show that ΔABC $\cong$ ΔCDA

Solution :

Provided data: p || q and l || m

Consider the triangles Δ ABC and Δ CDA

⇒ $\angle $BAC = $\angle $DCA

( Since p || q, the alternate interior angles are also equal. )

⇒ AC = CA

( AC is a common side to both triangles )

⇒ $\angle $DAC = $\angle $BCA

( Since l || m, the alternate interior angles are equal. )

∴ ΔABC $\cong$ ΔCDA

( by the ASA congruence rule. )

( According to the ASA (Angle-Side-Angle) congruence criterion, if two angles and the included side of one triangle are equal to the corresponding two angles and included side of another triangle, then the two triangles are congruent.)

Question 5

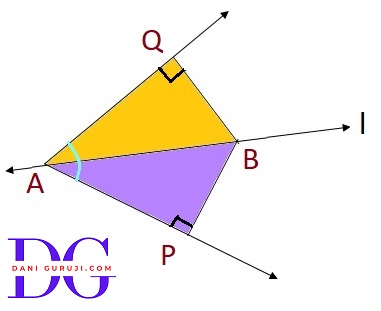
Line l is the bisector of an angle $\angle $A and B is any point on l. BP and BQ are perpendiculars from B to the arms of $\angle $A (see Fig.) Show that:
(i) Δ APB $\cong$ Δ AQB
(ii) BP = BQ or B is equidistant from the arms of $\angle $A.

Solution :

It is given that the line “l” is the bisector of angle $\angle $A and the line segments BP and BQ are perpendiculars drawn from l.

Consider the triangles ΔAPB and ΔAQB

⇒ $\angle $PAB = $\angle $QAB

( Line l is the angle bisector of $\angle $A, which means it divides the angle into two equal parts. Therefore, the angle formed by the arms of $\angle $A and the bisector are equal. )

⇒ $\angle $APB = $\angle $AQB

( BP and BQ are perpendiculars to the arms of $\angle $A. This means that $\angle $APB and $\angle $AQB are both right angles, and thus are equal. )

⇒ AB = AB

( AB is a common side to both triangles )

∴ Δ APB $\cong$ Δ AQB

( by the AAS congruence rule. )

( Since we have two pairs of equal angles and one pair of equal non-included sides (AAS congruence rule))

(ii)Proving BP = BQ

Because we have proven that Δ APB $\cong$ Δ AQB

we know that their corresponding parts are also equal.

BP and BQ are corresponding sides of the congruent triangles, we can say that BP = BQ. (By C.P.C.T.)

Or, it can be said that B is equidistant from the arms of $\angle $A.

Question 6

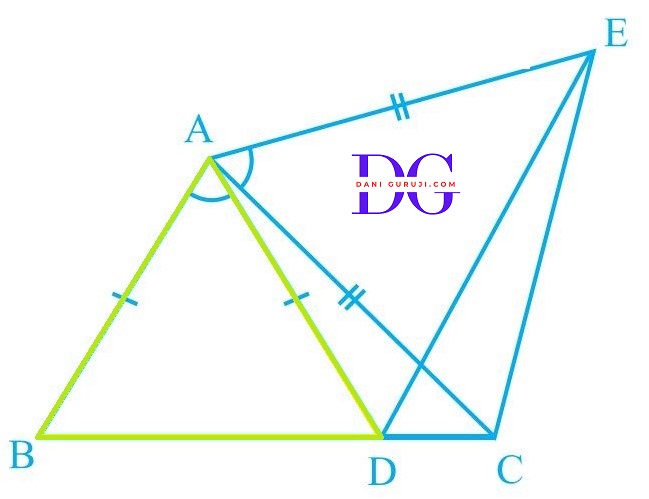
In figure, AC = AE, AB = AD and $\angle $BAD = $\angle $EAC. Show that BC = DE.

Solution :

Provided data :

AC = AE, AB = AD and $\angle $BAD = $\angle $EAC

Consider the triangles ΔABC and ΔADE

⇒ AC = AE

( As given in the question )

⇒ AB = AD

( As given in the question )

⇒ As it is given $\angle $BAD = $\angle $EAC

Adding $\angle $ DAC to both sides of this equation, we get :

$\angle $BAD + $\angle $ DAC = $\angle $EAC + $\angle $ DAC

$\angle $BAC = $\angle $DAE

( Proved here. )

∴ Δ ABC $\cong$ Δ ADE

( by the SSA congruence rule. )

( Since we have two pairs of equal sides and one pair of equal non-included angles (SSA congruence rule))

(i)Proving BC = DE

Because we have proven that Δ ABC $\cong$ Δ ADE

we know that their corresponding parts are also equal.

BC and DE are corresponding sides of the congruent triangles, we can say that BC = DE . (By C.P.C.T.)

Question 7

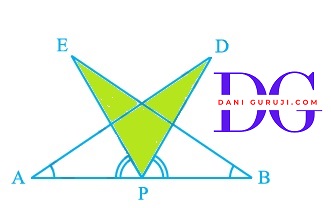
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that $\angle $BAD = $\angle $ABE and $\angle $EPA = $\angle $DPB (see Fig.). Show that:
(i) Δ DAP $\cong$ Δ EBP
(ii) AD = BE

Solution :

We are given that P is the midpoint of the line segment AB. This means that AP = BP.

We are also given that $\angle $BAD = $\angle $ABE and $\angle $EPA = $\angle $DPB.

Consider the triangles ΔDAP and ΔEBP

⇒ AP = BP

( given that P is the midpoint of AB )

⇒ $\angle $DAP = $\angle $EBP

( given that $\angle $BAD = $\angle $ABE )

⇒ We know that:

$\angle $DPA = $\angle $DPE + $\angle $EPA

$\angle $EPB = $\angle $DPE + $\angle $DPB.

Since $\angle $ EPA = $\angle $ DPB is given,

Adding $\angle $ DPE to both sides of this equation, we get :

$\angle $ DPE + $\angle $EPA = $\angle $ DPE + $\angle $DPB

$\angle $DPA = $\angle $EPB

( Proved here. )

∴ Δ DAP $\cong$ Δ EBP

( by the A.S.A congruence rule. )

(ii) Proving AD = BE

Because we have proven that Δ DAP $\cong$ Δ EBP

we know that their corresponding parts are also equal.

AD and BE are corresponding sides of the congruent triangles, we can say that AD = BE . (By C.P.C.T.)

Question 8

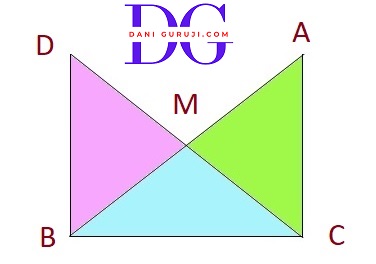
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that:
(i) ΔAMC $\cong$ Δ BMD
(ii) $\angle $DBC is a right angle
(iii) ΔDBC $\cong$ Δ ACB
(ii) CM = 1\2 AB

Solution :

(i) Proving Δ AMC $\cong$ Δ BMD

We are given that M is the midpoint of the line segment AB. This means that AM = BM.

We are also given that M is the midpoint of the line segment CD. This means that CM = DM.

Consider the triangles ΔAMC and ΔBMD

⇒ AM = BM

( given that M is the midpoint of AB )

⇒ CM = DM

( Given )

$\angle $AMC = $\angle $BMD

(These are vertically opposite angles. )

∴ ΔAMC $\cong$ Δ BMD

( by the SAS (Side-Angle-Side) congruence criterion. )

(ii) $\angle $DBC is a right angle

Since, ΔAMC $\cong$ Δ BMD

Therefore, $\angle $ACM = $\angle $BDM

(By C.P.C.T.)

$\angle $ACM and $\angle $BDM are alternate interior angles, Since alternate angles are equal, it can be said that, AC || BD.

Since AC is parallel to BD and BC is a transversal, the consecutive interior angles must sum to 180°.

$\angle $ACB + $\angle $ DBC = 180°

90°+ $\angle $ DBC = 180°

(We are given that $\angle $ ACB is a right angle, which means ∠ACB = 90° )

$\angle $ DBC = 180° - 90°

$\angle $ DBC = 90°

Thus, $\angle $ DBC is a right angle.

(iii) ΔDBC $\cong$ Δ ACB

Consider the triangles ΔDBC and ACB

⇒ DB = AC

(Since ΔAMC $\cong$ Δ BMD, DB and AC are corresponding sides, so by C.P.C.T, they are equal)

⇒ BC = BC

( Common Side )

$\angle $ACB = $\angle $ DBC

( Both are right angles, equal to 90°)

∴ ΔDBC $\cong$ Δ ACB

( by the SAS (Side-Angle-Side) congruence criterion. )

(iv) Proving CM = 1/2 AB

Since, ΔDBC $\cong$ Δ ACB (proven in part iii), the corresponding parts of the congruent triangles are equal. Therefore,

⇒ AB = DC (CPCT).

We know that M is the midpoint of DC (since DM = CM)

So, CM = 1/2 DC

Substituting DC with AB, we get:

CM = 1/2 AB

Thus, we have shown that CM is half the length of the hypotenuse AB